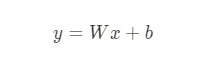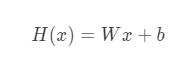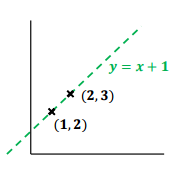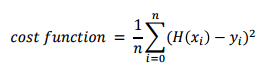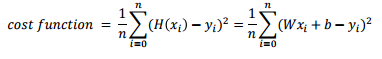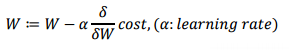반응형
선형회귀 실습
colab 이용하기 (구글에서 만든 주피터랑 비슷한 툴)
https://colab.research.google.com/notebooks/intro.ipynb#recent=true
파이참에 tensorflow-cpu 라이브러리 설치하기
→ 설치 안되면 파이썬 버전 낮춰서 Project 새로 만들기
- tensorflow , plot(그래프 그리는)을 하기 위한 라이브러리 import
- linear regression을 하기 위한 model 생성 - 클래스 활용해서 생성
- __init__ : 클래스 생성자
- 모델을 만들면 W, b 값을 5, 0으로 초기 셋팅이 되게 하는 생성자
- __call__ : tensorflow에서 짜면 자동으로 모델이 잘 호출이 된다.
- y = model(x) 이런식으로 호출 가능하다.
- __init__ : 클래스 생성자
import tensorflow as tf
import matplotlib.pyplot as plt
# linear regression model
class Model(object):
def __init__(self):
self.W = tf.Variable(5.0)
self.b = tf.Variable(0.0)
def __call__(self, x):
return self.W * x + self.b # 가설값
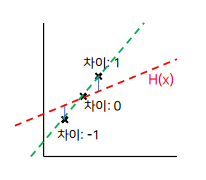
- MSE: Mean Squared Error
- 실제값과 가설값의 차이
- y : 실제값 , predicted : 가설값
- reduce_mean : 평균 구해주는 함수
- square : 제곱해주는 함수
# MSE: Mean Squared Error
def loss_function(y, predicted):
return tf.reduce_mean(tf.square(predicted - y))
- input을 random으로 만들고 w랑 b를 더하면 완전 선이 되니까 noise 를 더해준다.
- scatter 함수 → plt 라이브러리
- outputs : 실제값 , c : color
- model 함수 : 위에서 W와 b값을 미리 만들었기 때문에 그것에 대한 가설
- 실제 y값 = 3(실제 W값) * inputs(x값) + 2(실제 b값) + noise
model = Model()
true_w = 3.0 # 실제 W값
true_b = 2.0 # 실제 b값
examples = 1000 # 데이터 갯수
inputs = tf.random.normal(shape=[examples]) # input을 1000개 만든다.
noise = tf.random.normal(shape=[examples]) # noise를 1000개 만든다.
outputs = inputs*true_w + true_b + noise # 실제 y값
plt.scatter(inputs, outputs, c='b') # y - 파란선
plt.scatter(inputs, model(inputs), c='r') # H(x) - 빨간선
plt.show()
- outputs : 실제 y 값 , model(inputs) : 가설 h값
- 결과 Tensor 라는 함수로 반환을 하고 현재 loss는 8.85라고 출력
# loss function을 정의한 것에 대해서 loss값을 구해오는 것
loss = loss_function(outputs, model(inputs))
print(loss)
- GradientTape() 함수 : Tensorflow에 내장되어 있는 함수 사용
- gradient 를 직접 구하기가 힘드니까 직접 구해주는 함수
- gradient() 함수 호출하면 알아서 구해준다.
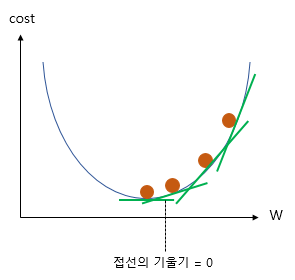
- 현재 loss를 기반으로 W와 b에 대해서 Gradient값을 구해주는 것
- gradient : 기울기
- assign_sub : Gradient Descent 과정에서 learning rate를 곱해서 적용
# Gradient Desent를 적용하는 과정
def train(model, inputs, outputs, learning_rate):
with tf.GradientTape() as t:
# loss function을 정의한 것에 대해서 loss값을 구해오는 것
current_loss = loss_function(outputs, model(inputs))
dW, db = t.gradient(current_loss, [model.W, model.b])
model.W.assign_sub(learning_rate*dW)
model.b.assign_sub(learning_rate*db)
- train() 함수 : 학습하는 함수
- 반복문을 돌면서 loss를 구해서 출력 , 반복 학습
- numpy() 함수 : loss_function의 loss값만 가지고 오는 함수
Ws, bs = [], [] # plot 저장할 변수
epochs = 15 # 학습데이터에 대해서 몇번 반복할지에 대한 변수
for epoch in range(epochs):
Ws.append(model.W.numpy())
bs.append(model.b.numpy())
current_loss = loss_function(model(inputs), outputs)
train(model, inputs, outputs, learning_rate=0.1)
print('epoch: %2d, W=%1.2f, b=%1.2f, loss=%2.5f'%(epoch, Ws[-1], bs[-1], current_loss))
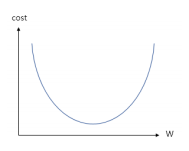
- W값과 b값을 찾아가는 과정을 나타낸 그래프
plt.plot(range(epochs), Ws, 'r', range(epochs), bs, 'b')
plt.show()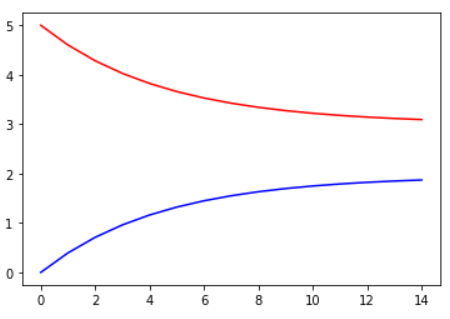
선형회귀분석을 1차원으로 봤는데 딥러닝에서는 수십 차원에 대해서 학습한다.
딥러닝에서는 선이 굴곡지게 그려지는데 실제로 제일 잘 맞는 선을 찾아야함.
너무 많이 돌리면 학습 데이터에 너무 학습이 된다.
노이즈가 조금 달라서 조금만 달라져도 값이 엄청 차이가 나면 실제 데이터에서 성능이 안나오게 된다.
→ 아주 많이 돌리면 Overfitting이 일어난다.
반응형
로지스틱 회귀
이진 분류(Binary Classification)
- 2가지중 하나를 선택하는 문제
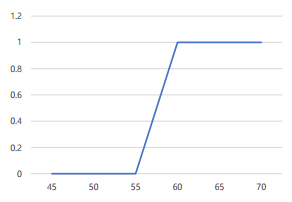
시그모이드 함수(Sigmoid Function)
- S자 형태로 그려지고, 0과 1 사이의 값을 가지는 함수
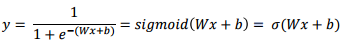
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y, 'g')
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()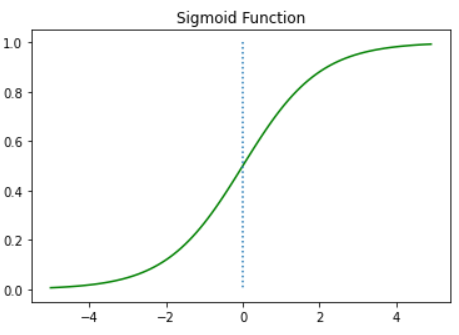
→ 0을 기준으로 0보다 클때는 1로 분류 , 0보다 작을때는 0으로 분류
→ 두개로 분류하는 logistic regression
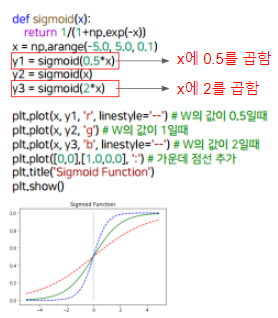
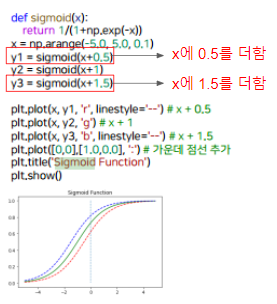
- 이런식으로 Sigmoid function이 움직이면서 분류에 맞게 점점 함수가 모양을 찾아감
- Linear Regression이 처음에 선을 점점 옮겨가면서 데이터에 맞게 찾아가는 것처럼 Rogistic Regression은 Sigmoid Function이 움직여가면서 두개로 분류를 할 수 있게 모델이 움직인다.
비용함수(Cost function or Loss function)
- 실제값이 1이고 예측값이 0일 때는 cost가 무한으로 발산 실제값이 0이고 예측값이 0일 때는 cost가 0
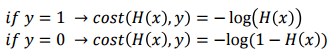
→ cost를 이런 식으로 지정을 해주면 위의 내용이 바로 반영이 된다.
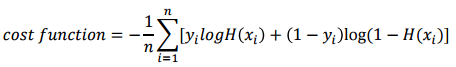
- 위에서 반영이 된 cost 값들을 다 더하게 cost function을 디자인을 한다.
- 이러한 cost function 을 cross entropy라고 함 → 분류에서 항상 사용이 됨 !! 중요한 부분
지금은 두개라서 0 ,1 인데 밀리면서 0 ,1 , 2 , 3 .. 이런식으로 디자인을 해서 멀티 클래스에서도 cross entropy를 기반으로 분류를 할 수 있음
Linear Regression이랑 Logistic Regression이 지금은 1차원으로 다루고 있지만 점점 2차원 , 3차원으로 올라가는게 딥러닝이다.
로지스틱 회귀 실습
import numpy as np
import tensorflow as tf
# numpy를 가지고 데이터를 임의로 만들어줌
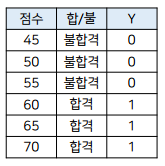
# 데이터가 - 일때는 0이 되고 , + 일때는 1로 분류
x = np.array([-5, -3, -1, 1, 3, 5])
y = np.array([0, 0, 0, 1, 1, 1])
- loss function 함수 정의
- y 값과 예측값(predicted 값)을 받아옴
- cost function 수식대로 짜준다.
# cross entropy loss function
def loss(y, predicted):
return tf.reduce_mean(-y*tf.math.log(predicted) - (1+y)*tf.math.log(1-predicted))
- 모델 생성
- W만 정의해준다. → W만 있던지 b랑 W랑 있던지 똑같은 과정임
class Model(object):
def __init__(self):
self.W = tf.Variable(-0.01)
def __call__(self, x):
return 1/(1+tf.math.exp(self.W*x))
model = Model()
- 학습 함수
- gradient 기울기 값 구해서 assign_sub 해줌
- assign_sub : Gradient Descent 과정에서 learning rate(학습률)를 곱해서 적용
# Gradient Desent를 적용하는 과정
def train(model, inputs, ouputs, learning_rate):
with tf.GradientTape() as t:
predict = model(inputs)
current_loss = loss(outputs, model(inputs))
dW = t.gradient(current_loss, model.W)
model.W.assign_sub(leaning_rate*dW)epochs = 10
for epoch in range(epochs):
current_loss = loss(y, model(x))
train(model, x, y, learning_rate = 0.01)
print("epoch:%2d, W=%1.2f, loss=%2.5f"%(epoch, model.W, current_loss))
→ epochs 값만큼 반복 학습함

→ 학습할수록 loss가 점점 줄어듬, W값 계속 변함
Linear Regression && Logistic Regression
머신러닝에서 제일 기초가 되는 과정이고 , 학습한 과정이 딥러닝 모델 학습하는 과정이랑 동일하고 좀더 복잡해지는 차이밖에 없음
꼭 잘 이해하고 넘어가야함 !!
반응형
'AI' 카테고리의 다른 글
| [AI] DNN(Deep Neural Network)이란? - 개념 및 실습 (0) | 2020.12.15 |
|---|---|
| [AI] 딥러닝 개요 - 순전파, 역전파 그리고 활성화 함수 (0) | 2020.12.15 |
| [AI] 딥러닝의 개요 - 퍼셉트론 (2) | 2020.11.27 |
| [AI] SVM 과 k-means clustering 이론 및 실습 (0) | 2020.11.27 |
| [AI] 인공지능의 개요 (0) | 2020.11.27 |